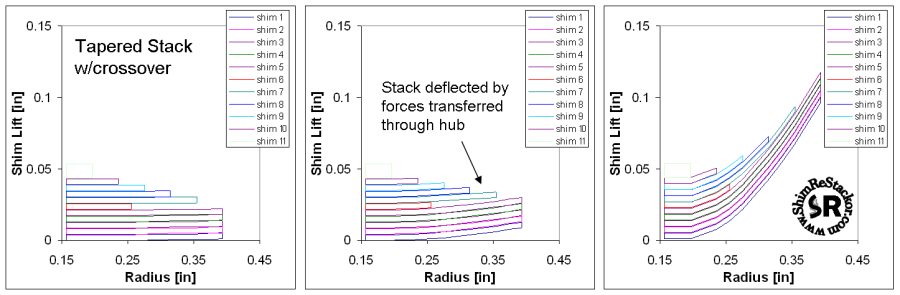
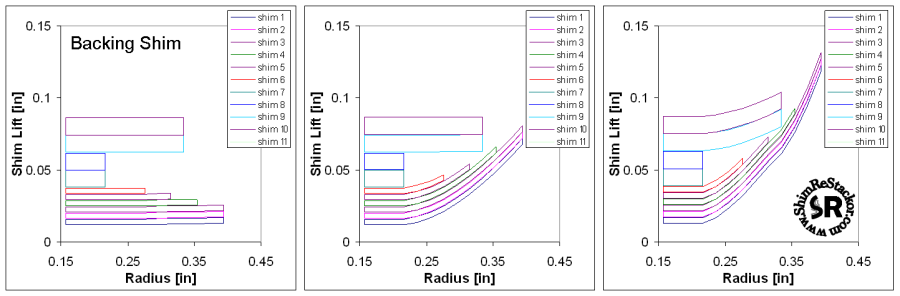
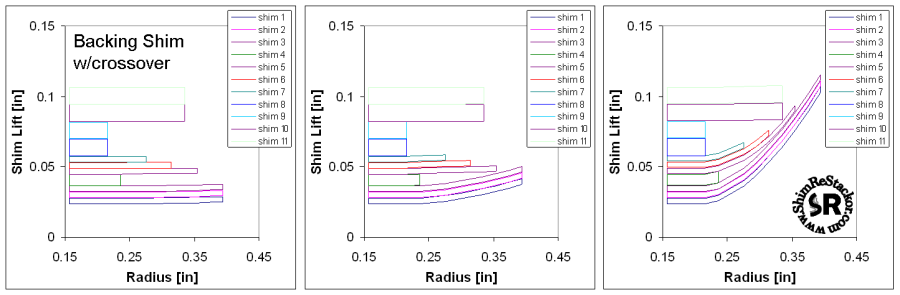
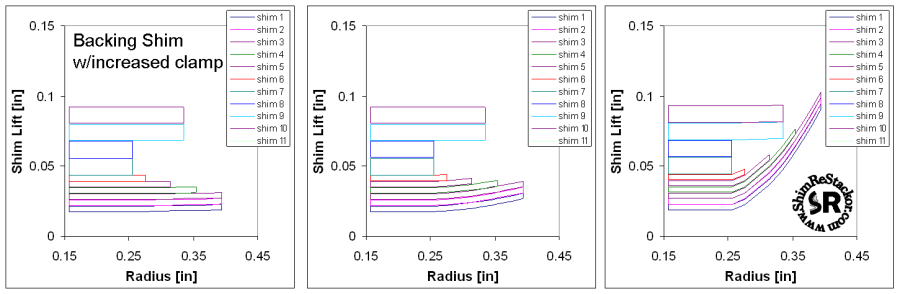
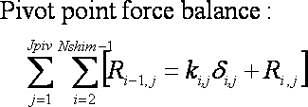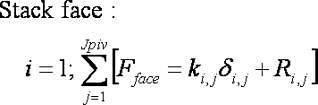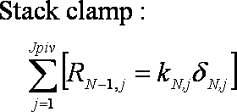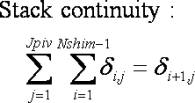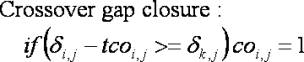Force balance

Shim Stack Force Balance
A central feature of ReStackor is the capability to accurately compute the stiffness of complex stack structures used in practical shim stack configurations. This requires construction of a force balance capable of accounting for effects of shim thickness, stack taper, clamp diameter, crossover shims, backing shims and the interactions of these features as the stack structure changes at different edge lifts. In addition, the force balance must also account for shifts in the location of the forces acting to deflect the stack caused by valve port geometry modifications. These effects are fully resolved in the thorough stack structure force balance used in ReStackor.
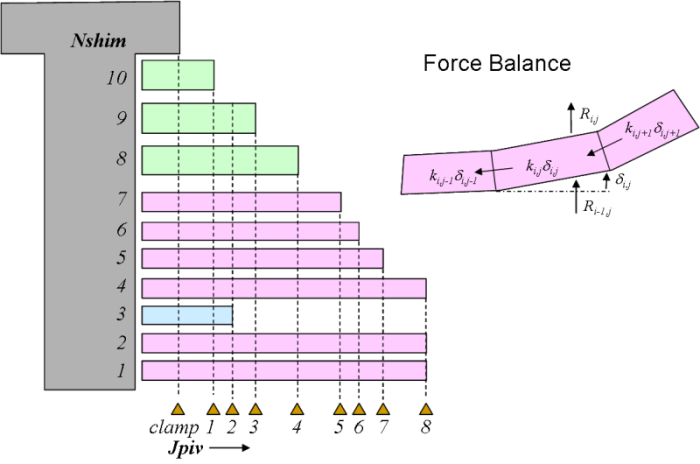
The nomenclature used in ReStackor force balance calculations is shown below for the classic case of a simple tapered stack with a crossover shim.
![]()
Force Balance Equations:
The above stack uses 10 shims with eight different diameters. A pivot point in the force balance is used at each shim diameter to resolve three forces. Forces reacted by the shim to the stack hub (ki,jdi,j), residual forces transferred from shims below the pivot point (Ri-1,j) and forces transfer to the shims above the pivot point (Ri,j).
The force on the face of the stack is specified by the valve fluid flow rate:
no forces are transferred out the top of the stack above the clamp shim:
The force balance contains JpivNshim variables for the shim deflection (di,j) and Jpiv(Nshim-1) residual force (Ri,j) variables. For these JpivNshim +Jpiv(Nshim-1) variables there are Jpiv(Nshim-2) force balance pivot points, plus Jpiv force specifications at the stack face and an additional Jpiv relationships for the stack clamp. This provides JpivNshim equations. The system of equations is closed by the addition of Jpiv(Nshim-1) continuity relationships for the stack:
A stack of 50 shims with 50 diameters results in JpivNshim +Jpiv(Nshim-1)= 4950 equations and 4950 variables. This same basic force balance has been used by Talbott[1] in his damper modeling work as well as Rhoades[2] Masters Thesis at Texas A&M.
The above relationships are adequate for a simple tapered stack. Application to practical suspension systems requires extension of these relationships to accommodate effects of crossover shims. For a crossover shim ReStackor evaluates closure of the crossover gap through the stack continuity relation:
Where tcoi,j is the crossover gap height and coi,j is a flag indicating the state of the gap. A crossover gap closes at the edge first. When closed, forces are transferred up the edge of the stack producing deflections of the shims above the crossover gap. As the stack loads increase more of the crossover gap is closed. This results in a continuously changing stack structure as the applied force is changed. ReStackor accurately tracks these forces allowing complex stack structures to be accurately computed.
[1] Talbott, M.S., and Starkey, J.,”An Experimentally Validated Physical Model of a High-Performance Mono-Tube Damper”, SAE 2002-01-3337, 2002.
[2] Rhoades, K.S.,”Development and Experimental Verification of a Parametric Model of an Automotive Damper”, Texas A&M Mechanical Engineering Masters Thesis, Aug 2006.
![]()
ReStackor
solver 4,950 simultaneous equations
A stack of 50 shims requires the solution of 4950 simultaneous equations. The force balance requires the forces at any point within the stack to be in balance with all of the forces below that point as well as all of the forces above that point. Due to this interaction the force balance at any given point can not be solved individually, the equations must all be solved simultaneously so that all forces within the stack are in balance with all of the other forces within the stack. Solving 4950 simultaneous equations is a daunting task if attempted by hand. Fortunately computers are extremely good at solution of simultaneous equations and sophisticated software packages have been developed to solve this type of problem.
ReStackor
uses sophisticated numerical techniques to solve the force balance equations
ReStackor use the Argonne National Labs BLAS[3] package to solve the 4950 simultaneous equations in the force balance. Solution of simultaneous equations in matrix form is a fundamental application for the computer industry. CPU speed are frequently quoted in terms of MFLOPS where a flop is the time required to solve a set of simultaneous equations in matrix form. Since CPU speeds are quoted in terms of MFLOPS the computer industry has funded numerous PhD thesis to optimize the speed of matrix inversions and produce robust software capable of quickly solving complex problems. These efforts have resulted in robust and highly efficient algorithms capable of solving matrix equations far beyond the complexity of the ReStackor force balance.
[3] BLAS: Univ. of Tennessee , Univ. of California Berkeley, NAG Ltd.,Courant Institute, Argonne National Lab and Rice University, March 31, 1993
![]()
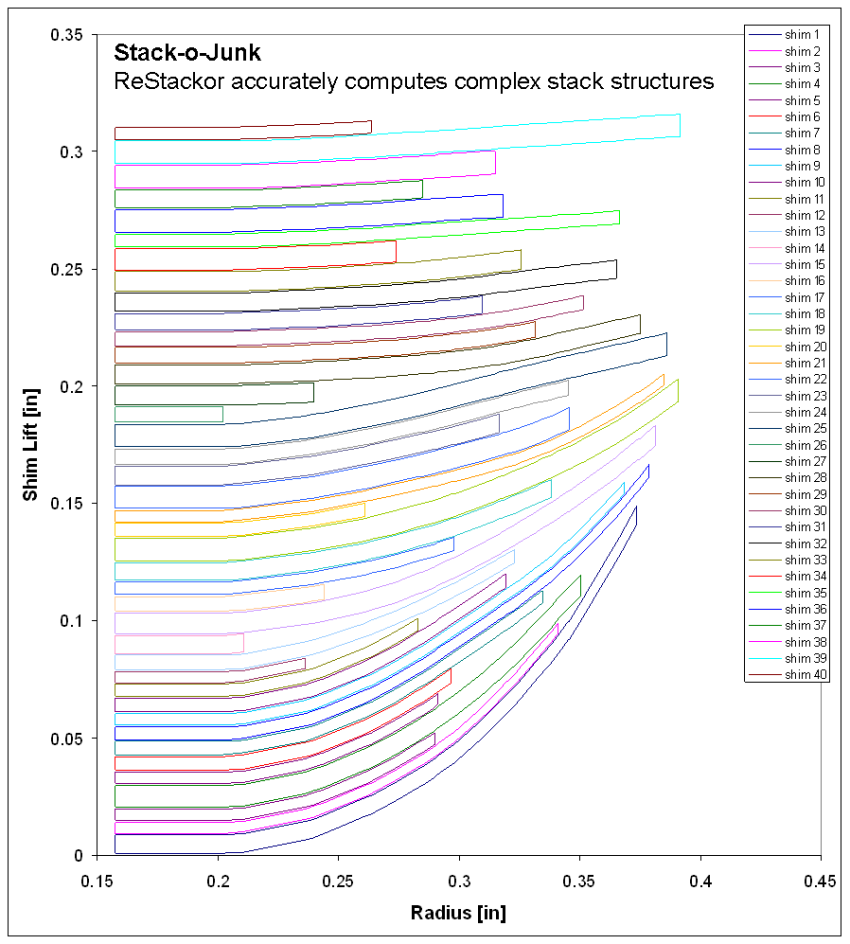
ReStackor capability to compute complex stack struchures demonstrated on a 40 shim "stack-o-junk"
To demonstrate the capability of ReStackor to accurately compute complex stack structures with multiple crossover points and variable stack stiffness the 40 shim "stack-o-junk" shown below was constructed. This stack was generated by a random number generator with variable shim diameters and variable shim thickness.
While not a practical suspension stack, the randomly varied shim diameters and random thickness used in this stack-o-junk produces multiple crossover gaps with varying heights and variable stack stiffness. Calculation of the force balance for this stack demonstrates the capability of the ReStackor to compute complex stack structures without zero divides, stack overruns or other software bugs inherent in complex applications. Deflection of the shims at the top of the stack are caused by forces transmitted through the stack hub. These forces deform the clamp shim into a cup shape and allow deflections of the large shims near the top of the stack. This effect could be eliminated through the use of a thicker clamp shim, but included here as an example of the transfer of forces through the stack.
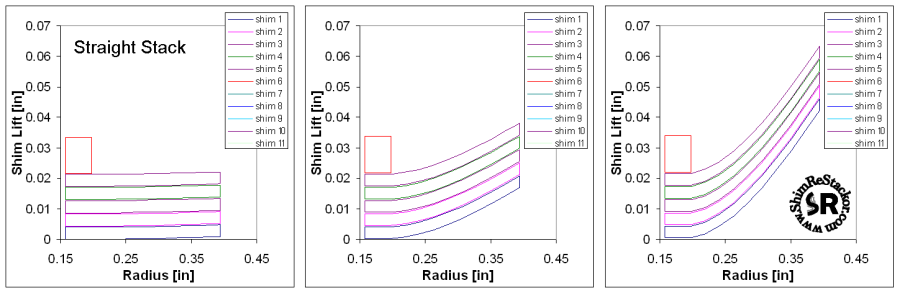
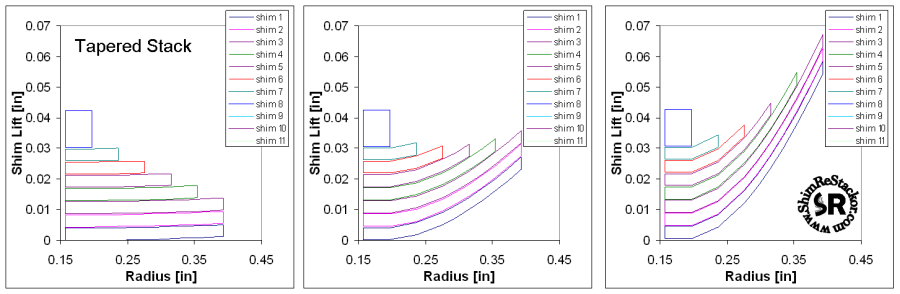
Beyond these debugging calculations ReStackor has also been anchored to dyno test data using real suspension hardware with practical shim stack configurations. Comparison with dyno data has demonstrated the capability of ReStackor calculations to not only accurately compute the stack force balance but also accurately compute the effect of stack stiffness on valve face flow area and its impact on suspension damping rates. Those comparison are reviewed in the dyno test section of the ReStackor web site. Some of the stacks configurations verified through dyno testing are shown below.