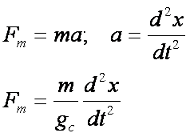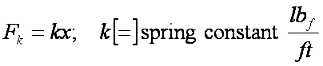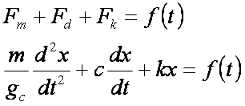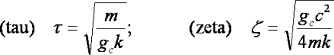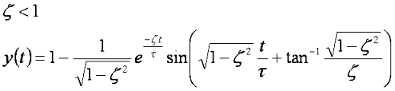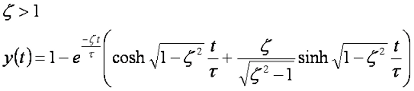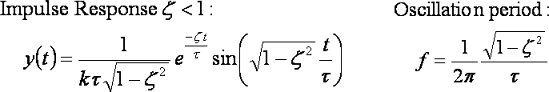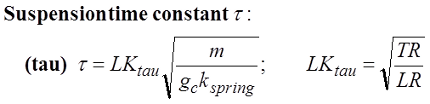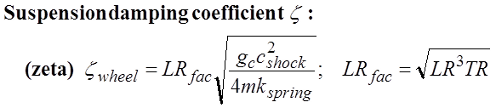Spring mass damper

Spring-Mass-Damper Systems
Suspension
Tuning
Basics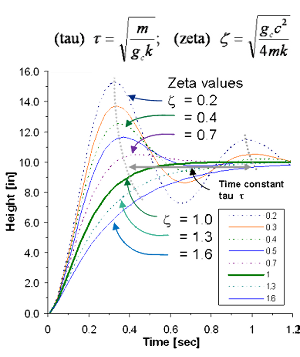
Controlling oscillations of a spring-mass-damper system is a well studied problem in engineering text books. Oscillation response is controlled by two fundamental parameters, tau and zeta, that set the amplitude and frequency of the oscillation. Those two parameters are simple functions of mass, spring rate and damping.
By spring-mass-damper theory two bikes of different weights and spring rates will retrace the exact same suspension response curve if the value of tau and zeta are set to be the same.
That basic physics provides a direct path to weight scale suspension performance from one bike to another and maintain the same suspension response, feel and behavior by compensating for differences in weight and spring rate by tuning the damping.
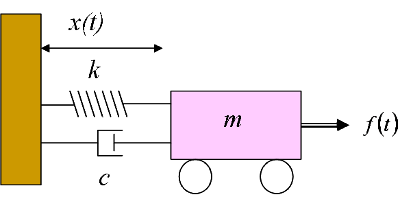
Spring-Mass-Damper System
The spring-mass-damper system consists of a cart with weight (m), a spring with stiffness (k) and a shock absorber with a damping coefficient of (c). The damping coefficient (c) is simply defined as the damping force divided by shaft velocity.
The equations describing the cart motion are derived from F=ma. The force required to accelerate the cart mass is:
and the force produced by the spring is:
The damping force from the shock absorber is described by the damping coefficient (c) multiplied by the shaft velocity:
Combining those terms into a force balance describes the cart motion as a function of position, velocity and acceleration:
The above equation describes the cart motion and includes effects of inertia as the cart is accelerated or decelerated, changes in spring force with stroke position and changes in damping force with shaft velocity. That equation describes all of the forces acting on the cart and the cart motion at any point in the oscillation.
![]()
Solution to the Equation of Motion for a Spring-Mass-Damper System
The equation describing the cart motion is a second order partial differential equation with constant coefficients. The fact the equation has a name is a clue that it is difficult to solve. Texts on control system theory work thorough the math of that so we won't muddle through that here. Instead, we jump to the solution equation written in terms of the oscillation time constant tau and a damping coefficient zeta:
If zeta is less than one (the usual case for suspensions) the cart motion is described by:
If zeta is greater than one the equation becomes:
On an impulse blow (a bump) the suspension response is described by:
Here is an important point: the above equation is not an approximation or estimate that sort-of follows the cart response. The above equation is exact in the same sense that F=ma is an exact description of the effect of force on acceleration.
Inspection of the equation gives some insight into how suspensions behave and the influence of tau and zeta on suspension performance. The equation for impulse response for zeta < 1 has the following behavior:
-
The sin term shows the response will be periodic with an oscillation frequency controlled by the value of tau.
-
The value of tau is defined by the ratio of mass to spring rate.
-
Stiffer springs will increase the oscillation frequency.
-
Increased weight will decrease the oscillation frequency.
-
If the ratio of mass to spring rate is the same the value of tau will be the same. In terms of suspension setup that tells you the suspension oscillation frequency will be the same if tau is the same, regardless of weight or spring rate.
-
-
The oscillation frequency is also influenced by the value of zeta, but with the zeta term buried inside the square root term the influence of zeta on oscillation frequency is weak.
-
The exponential term describes the rate of decay, ie damping.
-
At infinite time the negative term in the exponential forces the value of the exponential term to go to one indicating the suspension will return to its initial ride height after the oscillations die out (duh).
-
The zeta term in in the exponential controls the rate of decay. Increasing the damping coefficient increases the value of zeta making the decay faster.
-
The above behaviors are consistent with what you would intuitively expect from a suspension. The difference, and the reason for developing the equation, is the equation quantifies suspension response and defines the separate effects of spring rate, mass or damping changes on suspension response. That also allows evaluation of multiple simultaneous changes in spring rate, mass and damping on suspension response.
The more direct use of the equation is to determine the change in damping needed to keep suspension response the same. That comes down to adjusting damping to keep the value of zeta the same. Simple.
![]()
Suspension Response to a Step-Up
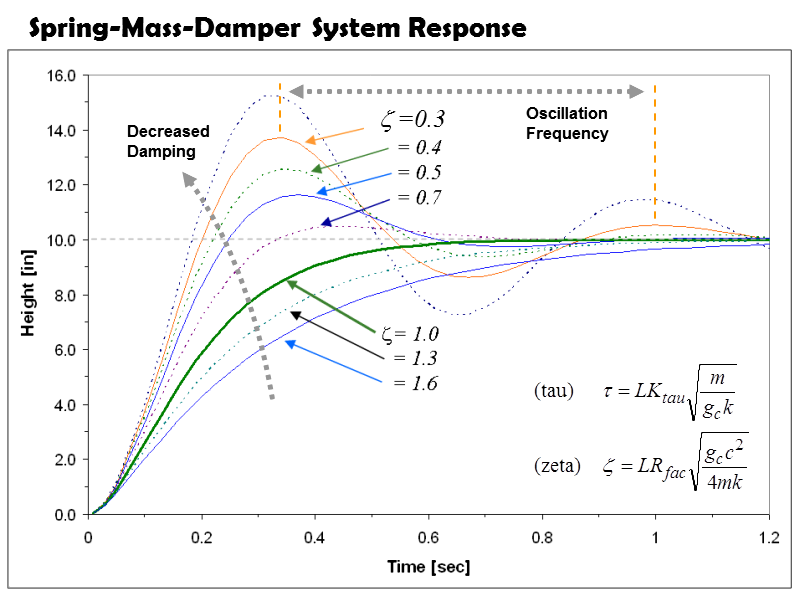
Suspension response for a sudden 10" step-up computed using the above equations is plotted below. Ideally the wheel would suddenly jump to the top of the 10" step and stay there with no oscillations. Because the wheel has mass it takes some time to vertically accelerate the wheel. Once moving, the momentum of the wheel causes the suspension to overshoot the top of the step. The combination of overshoot and wheel inertia cause the suspension to oscillate.
Suspension response as a function of time over a 10 inch step. Stiff damping slows the wheel response.
Under damped suspension response zeta<1:
If the suspension is under damped (zeta< 1) the suspension will oscillate and baby buggy a couple of times before settling down on top of the step. For a damping coefficient of 0.2 (zeta=0.2) the suspension will overshoot the 10" bump by about 5", then undershoot by 3" and baby buggy a couple more times before settling down on top of the step. All of this motion occurs within 1.2 seconds of hitting the bump.
Increasing the damping coefficient (zeta) decreases the overshoot as well as the oscillations. The down side is a heavily damped suspension takes longer to reach the top of a bump, you can see that in the above response curves. For the critically damped case (zeta=1) the suspension requires 0.8 seconds to respond to the 10" step. An under damped case with a damping coefficient of 0.4 responds to the same bump in 0.2 seconds, about 4 times faster. Four times faster response is a big deal in terms of plushness. If the wheel can not clear the bump then the bump ends up pounding directly into the bars.
Suspension Performance Basics
Spring-Mass-Damper theory defines two parameters, tau and zeta, that control suspension response.
Those parameters define the effect of mass, spring rate and damping on suspension performance. As long as the values of tau and zeta are the same the performance, response, feel and behavior of the suspension will be the same regardless of rider weight, spring rate or damping. Preserving suspension performance when the rider weight is changed requires changing both the spring rate and damping to keep the value of tau and zeta constant.
![]()
Weight Scaling a Stock Suspension
Modern motorcycles use sophisticated suspensions with independently adjustable compression, rebound, high speed and low speed damping. While the suspensions are sophisticated, mass production forces manufactures to build the suspension around the spring rate used in the stock suspension setup. That spring rate only matches one rider weight.
Changing spring rate to get your sag right drives the suspension into an under-damped or over-damped condition. Tau and zeta define the magnitude of that change and the path to restore suspension response to the performance the manufacturer intended for your bike.
Restoring performance requires modifying the shocks damping force to match the spring rate you are using and restore the factory value of zeta. Weight scaling is based on the following assumptions:
-
After winning several national championships and GP titles manufactures know something about how to setup MX and road race suspensions.
-
Some of that suspension tuning knowledge makes it from the track to production bikes.
-
Weight - spring rate - and damping are intimately coupled parameters that control suspension response through there effect on tau and zeta. The weight the stock suspension was designed for can be determined from the spring rate used in the stock setup.
-
The fundamentals of spring-mass-damper physics can be extracted from the ideal world of engineering theory to solve real world practical problems.
The suspension time constant (tau) is defined in terms of mass and spring rate. For a linked rear suspension the actual spring rate at the wheel is modified by the suspension travel ratio (TR) and link ratio (LR) creating the parameter LK.tau defined here.
Race sag is basically a measurement of weight over spring rate plus or minus some spring preload. Spring-mass-damper theory defines tau as the square root of the mass (m) divided by spring rate (k) making tau essentially equivalent to the square root of race sag. The unit conversion (g.c) in the tau equation relates the units of force to mass, it's a constant. When the bikes spring rate is changed to match the factory recommended race sag you are essentially setting up your suspension to match the factory value of tau.
The suspension damping rate is defined by zeta:
The added parameter in the zeta equation is the shock absorber damping coefficient (c) simply defined as the force produced by the shock divided by the shock shaft velocity. The effect of link ratio on zeta is summed up by the LR.fac term defined here. When the suspension spring constant (k), rider weight (m) or link ratio (TR, LR) is changed the damping coefficient (c) has to be modified to keep the value of zeta constant.
Switching to a stiffer spring for a heavier rider drives the value of zeta down making the suspension under-damped. Changing to a lighter spring for light weight rider drives the value of zeta up making the suspension over damped.
Frequency, amplitude and damping of any spring-mass-damper system will be identical, regardless of weight or spring rate, as long as the values of tau and zeta match. Correcting the value of zeta after a spring rate change requires damping to be modified to restore the initial value of zeta.
Correcting damping rates for a change in rider weight
The fix is simple. Whenever you change spring rate you have to modify the shocks damping coefficient (c) to keep the value of zeta constant at the value the manufacture intended for suspension response. The problem is nobody can tell you the value of the stock damping coefficient (c) or the shim stack modifications needed to correct damping for changes in spring rate.
That is where ReStackor comes in.
-
ReStackor can figure out the stock damping coefficient based on the shim stack configuration of the stock shock
-
For a given spring rate change the ReStackor weight scaling spreadsheet will show you the target damping force curve needed for a change in spring rate to keep the value of zeta constant.
-
All you have to do is hack around on the stock shim stack to match that target damping force curve.
ReStackor gives you the capability to correct suspension setups for changes in spring rate or scale suspension setups from one bike to another correcting for differences in suspension valve geometry, fluid viscosity and bleed circuits. That gives you the capability to correct the factory suspension setup for a change in weight or scale custom suspension setups from one bike to another bike that may be using a different valve port geometry.
ReStackor weight scaling example.
![]()
Weight Scaling Stock Suspension Damping Rates
The fundamentals of spring-mass-damper theory define two parameters that control suspension response. Tau defines the suspension oscillation time constant. The value of tau will be the same for riders of different weights if race sag is the same. Zeta defines the damping characteristics and relates the effect of weight, spring rate and damping to suspension response. Maintaining the suspension response, feel and behavior the manufacturer intended for your bike requires damping to be retuned after changing spring rates to restore the factory value of zeta.
In the end, performance comes down to how the suspension feels on the "butt dyno". After a couple of rides the "butt dyno" may tell you the high speed damping is too stiff or the low speed too soft. Experimenting with the clickers helps to quantify the damping force changes needed and ReStackor gives you the capability to relate those clicker changes to the specific shim stack modifications needed to match those clicker settings. The capability to experiment with the shim stack in software, match specific clicker settings and fine tune low and high speed damping gives you the capability to tune your suspension far beyond the limits previously possible.
ReStackor defines a new era in suspension tuning.